In several fields of mathematics, the terms combinations and permutations are used to specify the number of states generated for a given situation. Their difference relies on the ordering of the given objects when iterating through potential states. In particular, the number of permutations of a given state represents the number of all of the possible ways that a specified set of objects can be represented, whereas combinations do not repeat the same state in different order.

Texas Hold’em Poker Example [1]:

When calculating probabilities in the Texas Hold`em Poker, we only take into consideration the number of combinations rather than the number of permutations since the order in which the community cards are presented does not matter. The state {10♠, J♥, Q♣, K♦, A♠} is equivalent to {Q♣, 10♠, J♥, A♠, K♦}. The same applies when playing poker with more than one opponent since we do not care by whom we may lose, but only if we may lose.

Why is it important?

When calculating probabilities we save an enormous amount of time when processing and evaluating the different number of states since the number of combinations is equal to the number of permutations divided by the factorial of the number of objects. Assuming a total number of n objects available and r objects chosen, the equations for calculating combinations and permutations are respectively:

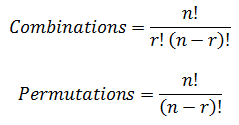
Further, there might be cases in which repetition of the objects is permitted. For example, if in a card game the state {K♦, J♥, Q♣, K♦, A♠} is possible, then repetition is permitted when generating the potential states; implying that an even larger number of states is to be generated for both combinations and permutations. Assuming a total number of n objects available and r objects chosen, the equations for calculating combinations and permutations with permitted repetition are respectively:

The calculator below will give you an idea of how massive the difference in states generated can be depending on the importance of the order and repetition.