|
|
Risk of Ruin Calculator
|
|
|
|
It is always wise to know the risks
involved with your initial bankroll when gambling or trading. The risk of ruin (also
known as the probability of ruin) refers to the probability of turning a
specified amount of money into nothing, and it is very popular amongst
professionals in Blackjack, Poker and financial traders; but also perfectly
suitable for many other forms of gambling. It appears that the Risk of Ruin was
first presented in [1] by the British statistician
David R. Cox
and Hilton D. Miller. The probability is calculated given your current bankroll,
the profit/win rate per trial/trade (or per minute/hour), and the standard
deviation of the winnings. This is expressed as:
|
|
|
|
|
|
|
|
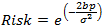
|
|
|
|
|
|
|
|
where e is the
Euler's Number ~2.7182, b
is the amount of money (bankroll) whose
risk of losing you are evaluating, p
is your profit ratio per trial and σ
is the standard deviation of winnings.
|
|
|
|
|
|
|
|
|
Bankroll |
(e.g. in €) |
|
|
|
Profit rate per trial |
(e.g. input of 0.10 for 10%) |
|
|
Standard Deviation of profit rate |
. |
|
|
|
|
|
|
|
|
|
|
|
|
With a bankroll of
N/A
,
a profit rate of
N/A
per trial, and a
σ
of
N/A
; your risk of ruin is
N/A
%.
|
|
|
|
|
|
|
|
|
Note that this calculator assumes that your profit rate
and standard deviation will not change over time; implying that the accuracy of
the result is dependent on the confidence of your inputs (e.g. you are much more
confident when your profit rate and standard deviation are determined by
thousands of trials rather that hundreds). Further, the resulting probability
refers to the specified risk for infinite amount of trials, which is considered
as a disadvantage by many since it is impossible for a gambler to bet/trade that
long. Despite the limitations, the generated result is a reasonable estimate for
controlling your risk and certainly superior to "advices". Alternatively, If you are looking for the size of bankroll required for
n probability of ruin, this is expressed as:
|
|
|
|
|
|
|
|
|
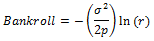
|
|
|
|
|
|
|
|
where e is the
Euler's Number ~2.7182, r
is the risk of ruin,
p is your profit ratio per trial, σ is the standard deviation of winnings and ln() is the
natural logarithm
|
|
|
|
|
|
|
|
|
Probability of risk of ruin |
(e.g. input of 0.10 for 10%) |
|
|
|
Profit rate per trial |
(e.g. input of 0.10 for 10%) |
|
|
|
Standard Deviation of profit rate |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
For a probability of ruin of
N/A
,
with a profit rate of
N/A
per trial, and with a
σ
of
N/A
; your required bankroll is
N/A
€.
|
|
|
|
_______________________________________ |
|
|
|
References
|
|
|
|
|
|
|
|
|
[1] |
Cox, D. R., & Miller, H. D. (1965). The theory of stochastic processes.
Methuen, London. |
|
|
|
|
|
|
|
|
___________________________________________________________________________________________ |
|
|
|
published online, 19/02/2012 |
|
|
|
|
|
|
|